Ground Control - aerial photograph
Ground Control
In order to produce an accurate map from aerial photograph it is absolutely necessary to established ground control. It consists in locating the positions of a no of pts. All over the area to be surveyed det their levels. These control pts short be such that can be easily identified on the photographs. Horizontal control is established by tiring or traversing. Vertical control is established through the use of ‘aneroid barometers’ or ‘Altimeters’
Applications of Air Photograph:
The practical uses of air photography are unlimited. Some of the application are listed below:
- Town and country planning and developed estate man agent and economic planning are used both maps based on air survey and individual photography’s.
- suitability of roads and rail alignments can be studied both for traffic flow an economy of construction.
- Forestry and geology both use air maps and photography for the study of nature of areas and changes that take place.
- Flood control planning can be based on air survey made at suitable intervals of time
- Air survey provides means of mapping large undeveloped areas of the world.
- For large scale engineering and redevelopment projects, reconnaissance can be undertake in to a large extend form air photograph.
- Survey for accessing damage due to earth quake, crop dieses can be quickly estimated from air photograph.
- Pollution effects form industrial wastes on land and water can be studied.
Tunnels:
Tunnels are constructed in order
- To meet the req of rapid transportation in big cities.
- To connect by shortest route, two termination separated by mountain.
- To reduce very steep grades.
- To avoid the excessive cost of mantaineice of an open cut subjected to land slides or snow drifts.
- To avoid the expensive acquisition of valuable built up land, tearing up pavements and holding up traffic for long periods in large cities
- When the depth of ordinary cutting exceeds 20m and the ground rises rapidly for a considerable distance after wards.
Chief considerations in location of a tunnel are
- If should follow the best line adopted to the proposed traffic.
- If should be most economical in construction an operation.
- Convenience Ingress (enter) and Egress (leave)
Tunneling involves the following operatios:
- Surface Survey
- Transferring the alignment under ground
- Transferring levels under ground
SURFACE SURVERY:
This includes
- A preliminary survey by transit and staid for 2-3miles (3-4km) on either side of the proposed alignment.
- A plan (map) with a scale of say 1 in with contours drawn at 5m (20) intervals.
- Final alignment is selected form this plan.
- A detail survey of the geological information of strata as the cost of tunneling depends upon the nature of materials to be encountered.
The proposed route having been decided upon, the following pts require consideration.
- Alignment of the centre line of the tunnel.
- Gradient to be adopted.
- Determination of the exact length of tunnel.
- Establishment of permanent stations marking the line.
Control surveys for tunnel layouts are performed on ht surface joining the terminal pts of the tunnel is shown in figure (1).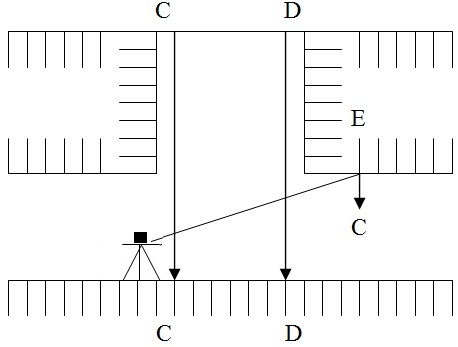
Transferring the alignment under ground:
This is the most difficult and important operation in setting out a tunnel.
- Fix two timber beams C and D as shown in figure two across the top of the shaft near its edges perpendicular to the direction of tunnel and as far apart as possible.
- A threadlike is set up at a ground at a pre-determined station on a centre. Line mark one ground surface and another stations is again on the centre line itself.
- The centre line is very carefully set up on the beams preferably on the plates fixed on a beam and drilled with hole for suspending wires by repetition observing and averaging the result.
- From these pts two long penal wire with heavy plumb hobs 10 to 15 kg attacked to their lower edges or suspended down the shaft.
- At the bottom these plumb bobs are immured in bucket of water, oil etc to eliminate oscillation.
- Great care must be taken that wires and plumb bobs are hanging free. As a check the dist b/w the wires at the top and at the bottom of the shaft is to be measured and this should be the same.
- The line joining the two wires gives the dir of alignment under ground.
- The theodolite is transfer to the bottom of shaft and through the no of trails suspended wires.
- Now the alignment is marked on marks driven into the whole i.e, E drilled on the roof.
Transferring levels under ground:
Leveling on the surface is done in the usual way and the levels are transfer underground at the ends of the tunnel from the nearest bench mark.
In case of transfer of levels underground at the shaft. The steps involve are
- A fine steel wire loaded with weight of 5 to 15 kg is passed over a pulley (w) at the top of the shaft and is lowered into the shaft as shown in fig.3
- Tow fine wire AA and BB horizontally stretched at the top and bottom of the shaft rasp.
- The steel wired lowered into the shaft is so adjusted that it is in contact with both the wires AA and BB.
- The pts of contact are marked on a still wire by a piece of chalk or by some other marker.
- The wire is withdrawn form the shaft and is stretched on the ground.
- The dist b/t the two marks on he wire is measured using the measuring tape and this gives the level of the bottom of the shaft.
LATTIUDE AND LONGITUDE:
O = Centre of earth
N = North Pole
S = South Pole
Nos = Polar axis or polar diameter about which earth rotates.
A = Any point on surface of earth
The position of a place on the earth surface is specified by latitude and longitude. The semi circle ‘NAS’ passing through A and terminates by the Poles N and S is called Meridian of the place.
LATITUDE:
Latitude of a place is the angular distance measured from the equator towards the nearer Pole along the meridian of the place or latitude of any pt ‘A’ is angle or arc AA’’. Latitude can also be defined as the angular distance that the place is north or south of equator.
The earth sphere being divided into two hemispheres by the equator, the upper one containing the North Pole is called the northern hemisphere. While the lower one having the South Pole is called southern hemisphere. The place is said to have a north latitude if it is in the northern hemisphere and south latitude if it is in the southern hemisphere.
The latitude angle is meared (90) at the earth center. North or south from the equatorial plane. Latitude north of equator is considered positive and that south of equator negative.
LONGITUDE:
Longitude of a place is the angular distance b/t the meridian of a place and the standard prime meridian
Or
Longitude of any place ‘A’ is angle ‘LA’ measured in the equatorial plane b/t the standard meridian and the meridian through A.
Or
The meridian NGS passing through Greenwich England has been adopted internationally as the standard meridian. This meridian divides the sphere into two hemispheres. The longitude is measured from “O” to 180 either towards east or west. The west longitude is considered as positive and the east as negative. Longitude angles are measured at the earth centre east or west from the plane of ‘O’ longitude which has been arbitrary placed through green witch England.
Hence the position of place ‘A’ is completely specified by the latitude and longitude. These two terms give unique location of any pt on the earth. This system of geographic co-ordinates is used in navigation and Geodesy.
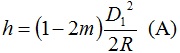
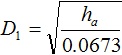Or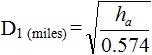 
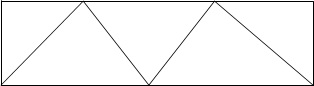Quadrilaterals pentagons or hexagonal with central stations. For very accurate work a chain of quadrilaterals may be used. There is no station at the intersection of diagonals. This system is most accurate since the number of conditions in its adjustments is much greater. To minimize the effect of small errors in measurement of angles the triangles hold be well shaped or well proportioned i.e. they should not have angle less than 30 or greater than 120.The best shape triangle is equilaterals triangle and best shape quadrilateral is square.