Solving spherical triangles

Solving spherical triangles Edit The general spherical triangle is fully determined by three of its six characteristics (3 sides and 3 angles). Note that the sides a, b, c of a spherical triangle are measured by angular rather than linear units, based on the corresponding central angles. The solution of triangles for non-Euclidean spherical geometry has some differences from the planar case. For example, the sum of the three angles α + β + γ depends on the triangle. In addition, there are no unequal similar triangles, and so the problem of constructing a triangle with specified three angles has a unique solution. The basic relations used to solve a problem are similar to those of the planar case: see Law of cosines (spherical) and Law of sines (spherical). Among other relationships that may be useful are the half-side formula and Napier's analogies:[7] {\displaystyle \tan {\frac {c}{2}}\cos {\frac {\alpha -\beta }{2}}=\tan {\frac {a+b}{2}}\cos {\frac {\alpha +\beta }{2}}} {\displaystyle \tan {\frac {c}{2}}\sin {\frac {\alpha -\beta }{2}}=\tan {\frac {a-b}{2}}\sin {\frac {\alpha +\beta }{2}}} {\displaystyle \cot {\frac {\gamma }{2}}\cos {\frac {a-b}{2}}=\tan {\frac {\alpha +\beta }{2}}\cos {\frac {a+b}{2}}} {\displaystyle \cot {\frac {\gamma }{2}}\sin {\frac {a-b}{2}}=\tan {\frac {\alpha -\beta }{2}}\sin {\frac {a+b}{2}}.}  Three sides given Three sides given (spherical SSS) Edit Known: the sides a, b, c (in angular units). The triangle's angles are computed from the spherical law of cosines: {\displaystyle \alpha =\arccos \left({\frac {\cos a-\cos b\ \cos c}{\sin b\ \sin c}}\right),} {\displaystyle \beta =\arccos \left({\frac {\cos b-\cos c\ \cos a}{\sin c\ \sin a}}\right),} {\displaystyle \gamma =\arccos \left({\frac {\cos c-\cos a\ \cos b}{\sin a\ \sin b}}\right).}  Two sides and the included angle given Two sides and the included angle given (spherical SAS) Edit Known: the sides a, b and the angle γ between them. The side c can be found from the law of cosines: {\displaystyle c=\arccos \left(\cos a\cos b+\sin a\sin b\cos \gamma \right).} The angles α', β can be calculated as above, or by using Napier's analogies: {\displaystyle \alpha =\arctan \ {\frac {2\sin a}{\tan({\frac {\gamma }{2}})\sin(b+a)+\cot({\frac {\gamma }{2}})\sin(b-a)}},} {\displaystyle \beta =\arctan \ {\frac {2\sin b}{\tan({\frac {\gamma }{2}})\sin(a+b)+\cot({\frac {\gamma }{2}})\sin(a-b)}}.} This problem arises in the navigation problem of finding the great circle between two points on the earth specified by their latitude and longitude; in this application, it is important to use formulas which are not susceptible to round-off errors. For this purpose, the following formulas (which may be derived using vector algebra) can be used: {\displaystyle {\begin{aligned}c&=\arctan {\frac {\sqrt {(\sin a\cos b-\cos a\sin b\cos \gamma )^{2}+(\sin b\sin \gamma )^{2}}}{\cos a\cos b+\sin a\sin b\cos \gamma }},\\\alpha &=\arctan {\frac {\sin a\sin \gamma }{\sin b\cos a-\cos b\sin a\cos \gamma }},\\\beta &=\arctan {\frac {\sin b\sin \gamma }{\sin a\cos b-\cos a\sin b\cos \gamma }},\end{aligned}}} where the signs of the numerators and denominators in these expressions should be used to determine the quadrant of the arctangent.  Two sides and a non-included angle given Two sides and non-included angle given (spherical SSA) Edit This problem is not solvable in all cases; a solution is guaranteed to be unique only if the side length adjacent to the angle is shorter than the other side length. Known: the sides b, c and the angle β not between them. A solution exists if the following condition holds: {\displaystyle b>\arcsin(\sin c\,\sin \beta ).} The angle γ can be found from the spherical law of sines: {\displaystyle \gamma =\arcsin \left({\frac {\sin c\,\sin \beta }{\sin b}}\right).} As for the plane case, if b < c then there are two solutions: γ and 180° - γ. We can find other characteristics by using Napier's analogies: {\displaystyle a=2\arctan \left[\tan \left({\tfrac {1}{2}}(b-c)\right){\frac {\sin \left({\tfrac {1}{2}}(\beta +\gamma )\right)}{\sin \left({\tfrac {1}{2}}(\beta -\gamma )\right)}}\right],} {\displaystyle \alpha =2\operatorname {arccot} \left[\tan \left({\tfrac {1}{2}}(\beta -\gamma )\right){\frac {\sin \left({\tfrac {1}{2}}(b+c)\right)}{\sin \left({\tfrac {1}{2}}(b-c)\right)}}\right].}  One side and two adjacent angles given A side and two adjacent angles given (spherical ASA) Edit
Three angles given (spherical AAA)Edit

Known: the angles α, β, γ. From the law of cosines we infer:

{\displaystyle a=\arccos \left({\frac {\cos \alpha +\cos \beta \cos \gamma }{\sin \beta \sin \gamma }}\right),}{\displaystyle b=\arccos \left({\frac {\cos \beta +\cos \gamma \cos \alpha }{\sin \gamma \sin \alpha }}\right),}{\displaystyle c=\arccos \left({\frac {\cos \gamma +\cos \alpha \cos \beta }{\sin \alpha \sin \beta }}\right).}

Solving right-angled spherical trianglesEdit

The above algorithms become much simpler if one of the angles of a triangle (for example, the angle C) is the right angle. Such a spherical triangle is fully defined by its two elements, and the other three can be calculated usingNapier's Pentagon or the following relations.

{\displaystyle \sin a=\sin c\cdot \sin A} (from the Law of sines (spherical)){\displaystyle \tan a=\sin b\cdot \tan A}{\displaystyle \cos c=\cos a\cdot \cos b} (from the law of cosines (spherical)){\displaystyle \tan b=\tan c\cdot \cos A}{\displaystyle \cos A=\cos a\cdot \sin B} (also from the law of cosines){\displaystyle \cos c=\cot A\cdot \cot B}

Some applicationsEdit

TriangulationEdit

Distance measurement by triangulation

Main article: Triangulation

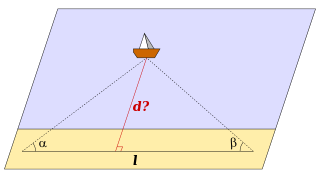
If one wants to measure the distance dfrom shore to a remote ship via triangulation, one marks on the shore two points with known distance lbetween them (the baseline). Let α, β be the angles between the baseline and the direction to the ship.

From the formulae above (ASA case) one can define the length of the triangle height:

{\displaystyle d={\frac {\sin \alpha \,\sin \beta }{\sin(\alpha +\beta )}}\,l={\frac {\tan \alpha \,\tan \beta }{\tan \alpha +\tan \beta }}\,l.}

This method is used in cabotage. The angles α, β are defined by observation of familiar landmarks from the ship.

How to measure a mountain's height

As another example, if one wants to measure the height h of a mountain or a high building, the angles α, β from two ground points to the top are specified. Let l be the distance between these points. From the same ASA case formulas we obtain:

{\displaystyle h={\frac {\sin \alpha \,\sin \beta }{\sin(\beta -\alpha )}}\,l={\frac {\tan \alpha \,\tan \beta }{\tan \beta -\tan \alpha }}\,l.}

The distance between two points on the globeEdit

Main article: Great-circle distance

To calculate the distance between two points on the globe,

Point A: latitude λ_A, longitude L_A, andPoint B: latitude λ_B, longitude L_B

we consider the spherical triangle ABC, where C is the North Pole. Some characteristics are:

{\displaystyle a=90^{\mathrm {o} }-\lambda _{\mathrm {B} },\,}{\displaystyle b=90^{\mathrm {o} }-\lambda _{\mathrm {A} },\,}{\displaystyle \gamma =L_{\mathrm {A} }-L_{\mathrm {B} }.\,}

If two sides and the included angle given, we obtain from the formulas

{\displaystyle \mathrm {AB} =R\arccos \left[\sin \lambda _{\mathrm {A} }\,\sin \lambda _{\mathrm {B} }+\cos \lambda _{\mathrm {A} }\,\cos \lambda _{\mathrm {B} }\,\cos \left(L_{\mathrm {A} }-L_{\mathrm {B} }\right)\right].}

Here R is the Earth's radius.