Solving plane triangles
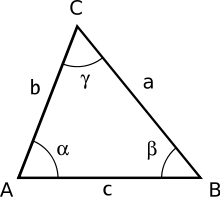
A general form triangle has six main characteristics (see picture): three linear (side lengths a, b, c) and three angular (α, β, γ). The classical plane trigonometry problem is to specify three of the six characteristics and determine the other three. A triangle can be uniquely determined in this sense when given any of the following:
- Three sides (SSS)
- Two sides and the included angle (SAS)
- Two sides and an angle not included between them (SSA), if the side length adjacent to the angle is shorter than the other side length.
- A side and the two angles adjacent to it (ASA)
- A side, the angle opposite to it and an angle adjacent to it (AAS).
- Three angles (AAA) on the sphere (but not in the plane).
For all cases in the plane, at least one of the side lengths must be specified.
If only the angles are given, the side lengths cannot be determined, because any similar triangle is a solution
Trigonomic relations

The standard method of solving the problem is to use fundamental relations.
- Law of cosines
- Law of sines
- Sum of angles
- Law of tangents
There are other (sometimes practically useful) universal relations:
the law of cotangents and Mollweide's formula.
Notes
- To find an unknown angle, the law of cosines is safer than the law of sines. The reason is that the value of sine for the angle of the triangle does not uniquely determine this angle. For example, if sin β = 0.5, the angle β can equal either 30° or 150°. Using the law of cosines avoids this problem: within the interval from 0° to 180° the cosine value unambiguously determines its angle. On the other hand, if the angle is small (or close to 180°), then it is more robust numerically to determine it from its sine than its cosine because the arc-cosine function has a divergent derivative at 1 (or −1).
- We assume that the relative position of specified characteristics is known. If not, the mirror reflection of the triangle will also be a solution. For example, three side lengths uniquely define either a triangle or its reflection.
Three sides given (SSS)
Let three side lengths a, b, c be specified. To find the angles α, β, the law of cosines can be used:
Then angle γ = 180° − α − β.
Some sources recommend to find angle β from the law of sines but (as Note 1 above states) there is a risk of confusing an acute angle value with an obtuse one.
Another method of calculating the angles from known sides is to apply the law of cotangents.
Two sides and the included angle given (SAS)
Here the lengths of sides a, b and the angle γ between these sides are known. The third side can be determined from the law of cosines:
Now we use law of cosines to find the second angle:
Finally, β = 180° − α − γ.
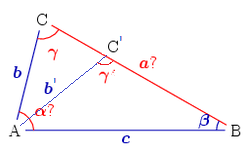
Two sides and non-included angle given (SSA)
This case is not solvable in all cases; a solution is guaranteed to be unique only if the side length adjacent to the angle is shorter than the other side length. Assume that two sides b, c and the angle β are known. The equation for the angle γ can be implied from the law of sines:
We denote further D = cb sin β (the equation's right side). There are four possible cases:
- If D > 1, no such triangle exists because the side b does not reach line BC. For the same reason a solution does not exist if the angle β ≥ 90° and b ≤ c.
- If D = 1, a unique solution exists: γ = 90°, i.e., the triangle is right-angled.
- If D < 1 two alternatives are possible.
- If b ≥ c, then β ≥ γ (the larger side corresponds to a larger angle). Since no triangle can have two obtuse angles, γ is an acute angle and the solution γ = arcsin D is unique.
- If b < c, the angle γ may be acute: γ = arcsin D or obtuse: γ′ = 180° - γ. The figure on right shows the point C, the side b and the angle γ as the first solution, and the point C′, side b′ and the angle γ′ as the second solution.
Once γ is obtained, the third angle α = 180° − β − γ.
The third side can then be found from the law of sines:
or
A side and two adjacent angles given (ASA)
The known characteristics are the side c and the angles α, β. The third angle γ = 180° − α − β.
Two unknown side can be calculated from the law of sines:
or






![{\displaystyle {\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b7a4a3592aa66976f1d34bbbb403daa392f9fdf)

![{\displaystyle {\begin{aligned}\alpha &=\arccos {\frac {b^{2}+c^{2}-a^{2}}{2bc}}\\[4pt]\beta &=\arccos {\frac {a^{2}+c^{2}-b^{2}}{2ac}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/468caceefca9cadbcccf4071a44d9c3107dd5b33)











No comments:
Post a Comment