Simpson's Rule
by M. Bourne
Interactive exploration
See an applet where you can explore Simpson's Rule and other numerical techniques:
Riemann Sums AppletIn the last section,
Trapezoidal Rule, we used
straight lines to model a curve and learned that it was an improvement over using rectangles for finding areas under curves because we had much less "missing" from each segment.
We seek an even better approximation for the area under a curve.
In
Simpson's Rule, we will use
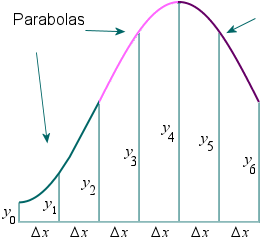
parabolas to approximate each part of the curve. This proves to be very efficient since it's generally more accurate than the other numerical methods we've seen. (See more about
Parabolas.)
We divide the area into
n equal segments of width
Δx. The approximate area is given by the following.
Note: In Simpson's Rule, n must be EVEN.
See below how we obtain Simpson's Rule by finding the area under each parabola and adding the areas.
Memory aid
We can re-write Simpson's Rule by grouping it as follows:
∫abf(x)dx ≈3Δx[y0+4(y1+y3+y5+…) +2(y2+y4+y6+…)+yn] This gives us an easy way to remember Simpson's Rule:
∫abf(x)dx ≈3Δx[FIRST+4(sum of ODDs) +2(sum of EVENs)+LAST Example using Simpson's Rule
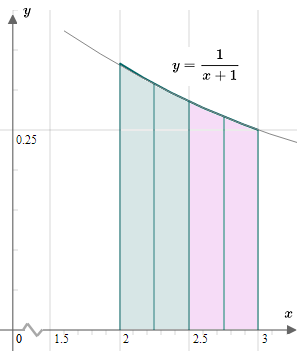
Approximate
∫23x+1dx using Simpson's Rule with
n=4.We haven't seen how to integrate this using algebraic processes yet, but we can use Simpson's Rule to get a good approximation for the value.
Here is the situation.
Δx=nb−a=43−2=0.25 y0=f(a) =f(2) =2+11=0.3333333 y1=f(a+Δx)=f(2.25) =2.25+11=0.3076923 y2=f(a+2Δx)=f(2.5) =2.5+11=0.2857142 y3=f(a+3Δx)=f(2.75) =2.75+11=0.2666667 y4=f(b)=f(3) =3+11=0.25 So
Area
=∫abf(x)dx≈30.25(0.333333+4(0.3076923) +2(0.2857142)+4(0.2666667) +0.25) =0.2876831
Notes
1. The actual answer to this problem is 0.287682 (to 6 decimal places) so our Simpson's Rule approximation has an error of only 0.00036%.
2. In this example, the curve is very nearly parabolic, so the 2 parabolas shown above practically merge with the curve
y=x+11.

No comments:
Post a Comment